Prékopa András
Bolyai János forradalma
Harmadik rész
A Bolyai–Lobacsevszkij-geometria fogadtatása és utóélete
 Lobacsevszkij
közleményeit a szakmai és a nem szakmai közvélemény egyaránt érdektelenséggel
fogadta. Bolyainál nem ez volt a helyzet, ő még letaglózást is kapott hozzá,
Gausstól. Ám másoknak azért lehetett pozitív véleménye Bolyai művéről.
Talán a leghivatottabb testület, a Magyar Tudós Társaság Mathematikai Osztálya
kifejezte valamiképpen elismerését? Vállas Antal akadémikus 1836-ban összefoglaló
cikket írt a hazai matematika addigi eredményeiről. Hosszasan panaszkodik,
hogy nehéz sorsunk volt; tatár, török stb., ezért nem tudtunk eléggé fejlődni.
Bolyaival kapcsolatban idézi a Tentamen, Az arithmetica eleje és Az arithmeticának,
geometriának és physikának eleje című műveket. A szövegben csak annyit
ír, hogy „Bolyai különcségével tűnik ki”. A művek felsorolásából látjuk,
hogy Farkasról, nem pedig Jánosról van szó. Ámde a Tentamen címében benne
van, hogy „Cum Appendice Triplici”, tehát valamiképpen mégis szerepel János
műve is a felsorolásban? Sajnos, ez sem áll. Az említett három függelék
a második kötethez tartozik, vagyis a teljes könyv végén van. A Tentamenhez
készített magyar nyelvű prospektus tájékoztatta a vásárlókat arról, hogy
a jelzett három függelék hol található. E szerint Bolyai János művét Vállas
Antal összefoglaló cikke nem említi, az irodalomjegyzékben sem szerepel.
Azt, hogy az összefoglaló cikk szerzője nem értette meg Bolyai János alkotásának
lényegét és jelentőségét, még el lehet fogadni. Azt azonban már nem, hogy
említést sem tesz róla. Pedig Bolyai Farkas a Tentament 1832-ben megküldte
a Magyar Tudós Társaságnak, és az ott porosodott a könyvtár polcain.
Lobacsevszkij
közleményeit a szakmai és a nem szakmai közvélemény egyaránt érdektelenséggel
fogadta. Bolyainál nem ez volt a helyzet, ő még letaglózást is kapott hozzá,
Gausstól. Ám másoknak azért lehetett pozitív véleménye Bolyai művéről.
Talán a leghivatottabb testület, a Magyar Tudós Társaság Mathematikai Osztálya
kifejezte valamiképpen elismerését? Vállas Antal akadémikus 1836-ban összefoglaló
cikket írt a hazai matematika addigi eredményeiről. Hosszasan panaszkodik,
hogy nehéz sorsunk volt; tatár, török stb., ezért nem tudtunk eléggé fejlődni.
Bolyaival kapcsolatban idézi a Tentamen, Az arithmetica eleje és Az arithmeticának,
geometriának és physikának eleje című műveket. A szövegben csak annyit
ír, hogy „Bolyai különcségével tűnik ki”. A művek felsorolásából látjuk,
hogy Farkasról, nem pedig Jánosról van szó. Ámde a Tentamen címében benne
van, hogy „Cum Appendice Triplici”, tehát valamiképpen mégis szerepel János
műve is a felsorolásban? Sajnos, ez sem áll. Az említett három függelék
a második kötethez tartozik, vagyis a teljes könyv végén van. A Tentamenhez
készített magyar nyelvű prospektus tájékoztatta a vásárlókat arról, hogy
a jelzett három függelék hol található. E szerint Bolyai János művét Vállas
Antal összefoglaló cikke nem említi, az irodalomjegyzékben sem szerepel.
Azt, hogy az összefoglaló cikk szerzője nem értette meg Bolyai János alkotásának
lényegét és jelentőségét, még el lehet fogadni. Azt azonban már nem, hogy
említést sem tesz róla. Pedig Bolyai Farkas a Tentament 1832-ben megküldte
a Magyar Tudós Társaságnak, és az ott porosodott a könyvtár polcain.
Alexits (1977) említi, hogy a Magyar Tudós Társaság Mathematikai Osztálya
1844-ben pályadíjként kitűzte a paralelák problémáját. Ez azonban nem felel
meg a valóságnak. Az 1844. évi „jutalomtétel”, melyet az 1844. december
26-ai nagygyűlésen elfogadtak, a következő: „Mik a képzetes mennyiségek
tulajdonságai, s mind analyticai, mind mértani értelmök?” Jóllehet erre
vonatkozólag is volt Bolyai Jánosnak, sőt Farkasnak is munkája, ezt egyikük
sem publikálta, csupán megküldte a lipcsei Jablonowski Társaságnak, ugyancsak
pályadíj elnyerése céljából. A Tudós Társaság matematikusai e tekintetben
tehát nem hibáztathatók. Ács Tibor (1998) cikkében részletesen beszámol
e pályadíj keletkezésének történetéről. Ebben az időben a hadtudomány a
matematikai osztályon belül volt, és Kiss Károly százados, az osztály hadtudománnyal
foglalkozó tagja szerette volna, ha 1844-ben hadtudományi pályadíjat tűznek
ki. Javaslatának szövegében egy északról érkező támadás esetére vonatkozó
védelmi terv kidolgozása szerepel. Ezzel akarta elérni azt, hogy a hadtudomány
az akadémiai osztályon belül megbecsültebbé váljék. Törekvése azonban sikertelen
maradt és végül az említett pályadíjat tűzték ki.
A hivatalosak tehát nem érdeklődtek Bolyai János műve után, de mások
se nagyon. Idézzünk Bolyai Farkas 1836. október 3-án kelt, Gausshoz intézett
leveléből: „Itt senkinek sem kell a Matematika; tanítványaim közül csak
kevésnek van igazi érzéke hozzá, művemet makulatúrának, csomagolásra és
hasonlókra használom, kiváltképp hasznomra volt az itt nemrégiben dühöngő
kolera idején, amiben én is szenvedtem egy hónapig, de hányás és görcs
nélkül, csak szerfelett levert voltam, undorodtam az ételtől és bortól,
kínzó szomjúság gyötört friss vízre és nagy diarrhoe-m volt, most is hasmenésem
van”. (Bolyai-levelek, 1975., 188. old.)
Bolyai János műve felfedezésének története külföldön kezdődött. Ebben
nagy szerepet játszott Gauss 1855-ben bekövetkezett halála után hagyatékának
a feldolgozása. Megtalálták Bolyai, Lobacsevszkij műveit, Gauss másokhoz,
és mások Gausshoz intézett leveleit. A hagyatékot Sartorius von Waltershausen
göttingeni professzor rendezte, akinek Bolyai Farkas is megküldte Gaussnak
hozzá intézett leveleit, így azok is a hagyatékba kerültek. Lassan bontakozni
kezdett a kép.
Az első, nyomtatásban megjelent elismerő szavak a drezdai matematikaprofesszortól,
Baltzertől származtak, ezeket az 1866–67-ben megjelent Elemente der Mathematik
című, jól ismert és befolyásos könyvében írta le. Ezt követően Hoüel bordeaux-i
professzor kiadott egy brosúrát „Essai critique sur les principes fondamentaux
de la Géometrie élémentaire” címmel, melyben kivonatokat közölt az Appendixből,
„hogy biztosítsa ezeknek az új gondolatoknak az elismerését, melyet azok
megérdemelnek”. Az utóbbi idézet Schmidt Ferenc budapesti építésztől származik,
aki 1868-ban cikket írt a két Bolyai életéről. Az övé volt az első magyarországi
reagálás, közel negyven évvel a Tentamen és az Appendix megjelenése után.
Hoüel 1867-ben az Appendix teljes francia nyelvű fordítását is kiadta,
mellékelve hozzá Schmidt Ferencnek a Bolyaiakról írt életrajzát. Így került
Höuel könyvébe a fenti idézet.
Az 1868-as év meghozta az érdeklődést mások részéről is. Ebben az évben
jelent meg az olasz Beltrami cikke, melyben modellt adott a Bolyai–Lobacsevszkij-geometria
számára. A két pionír ugyanis nyitva hagyta axiómarendszere ellentmondás-mentességének
kérdését. Ezt a kérdést oly módon lehet megválaszolni, hogy az axiómákban
nem értelmezett fogalmakat (pont, egyenes, sík) konkrét tartalommal töltjük
meg, modellt adunk az új geometria számára. Ha legalább egy modell létezik,
akkor az axiómák ellentmondásmentesek, van értelme a dolognak. A modell,
ahogyan a nemeuklideszi geometria történetét tárgyaló szerzők ironikusan
megjegyzik, az euklideszi geometrián belül helyezkedik el.
Riemann 1854-ben fektette le geometriájának alapjait. Riemann, aki Gauss
tanítványa volt Göttingenben, geometriáját a Gauss által korábban kidolgozott
felületelméletre alapozta. A Riemann-geometria megértése és elismerése
nem okozott gondot a német és a nemzetközi matematikai életben. Beltrami,
aki a Bolyai–Lobacsevszkij-geometriát a Riemann-geometria keretei között
helyezte el, ezáltal is nagyban hozzájárult a hiperbolikus geometria útjának
egyengetéséhez. Innentől már fel is fokozódott az érdeklődés. A kor nagy
matematikusai, Poincaré, Klein, Fuchs és mások publikáltak új modelleket,
további eredményeket. Ennek kapcsán új matematikai tudományok is születtek.
Sajnos azonban inkább csak Lobacsevszkijre hivatkoztak, Bolyai nemzetközi
elismertetése későbbre maradt.
Ezen a ponton tesszük fel a kérdést: széles körben megértették-e a tudomány
képviselői – elsősorban a matematikusok, legalább évtizedekkel a felfedezés
után – Bolyai és Lobacsevszkij művének igazi jelentőségét? Cayley (1821–1895),
aki egy időben a British Association elnöke volt, 1883 szeptemberében tartott
elnöki beszédében így nyilatkozott: „Jól ismert, hogy Eukleidész tizenkettedik
axiómáját Playfair formájában is bizonyításra szorulónak tekintették; és
hogy Lobacsevszkij egy olyan tökéletesen konzisztens elméletet konstruált,
nem euklideszi síkgeometriát, melyben ez az axióma érvénytelennek van feltételezve.
Van egy hasonló nemeuklideszi szilárd (solid) geometriai rendszer is. Az
én nézetem az, hogy Eukleidész axiómájának Playfair formája nem igényel
bizonyítást, hanem az része a térfogalmunk fizikai terének – a térnek,
mellyel tapasztalat útján ismerkedünk meg és mely alapvetően a külső tapasztalat
reprezentációja.”
Cayley az Elemek olyan kiadását ismerte, melyben az V. posztulátum tizenkettedik
axiómaként szerepel. Playfair axiómája, mint említettük, az V. posztulátummal
egyenértékű. Cayley idézetében érezhető Kant hatása. A lényeg azonban az,
hogy a nemeuklideszi geometriának szerinte semmi értelme, hiszen a világ
euklideszi.
Gauss 1855-ben bekövetkezett haláláig a tudományos világ Lobacsevszkij
munkáját sem méltatta figyelemre. Pedig ő 1840-ben német nyelven is közzétette
eredményeit, és az ő irányába Gauss nem fukarkodott az elismeréssel, bár
ezt csak levélben tette meg, nyomtatott írásban nem. Mindamellett más módon
kifejezte nagyrabecsülését, Lobacsevszkijt 1842-ben megválasztatta a Göttingeni
Királyi Társaság külföldi levelező tagjává. Otthon, Oroszországban azonban
forradalmi elmélete miatt félreállították. Karrierje ígéretesen kezdődött,
fiatalon, huszonhárom éves korában professzor lett a kazányi egyetemen,
tizenegy évvel később, 1827-ben pedig ugyanott rektor is lett. Egyetemének
fejlesztésén sokat fáradozott, igen eredményesen. Az 1830-ban kitört kolerajárvány
idején sikerrel védte meg az egyetem tanárait, családjukat és a hallgatóságot
a járványtól, közöttük csak 2,5 százalékos volt a halálesetek száma. Mindezek
ellenére 1846-ban, ötvennégy éves korában, minden magyarázat nélkül felmentették
a rektori megbízatása, sőt a professzori állása alól is. Talán Bolyai is
hasonló sorsra jutott volna, ha sikerül hazájában tehetségéhez és tudományos
eredményeihez méltó professzori állást kapnia? Lobacsevszkij életéről és
munkásságáról Kárteszi Ferenc (1953) írt magyar nyelven cikket.
Cayley kantiánus szellemet tükröző idézete után lássuk, mit ír Riemann
a geometriai térfogalomról. Az 1854-ben Göttingenben megtartott és 1868-ban
publikált magántanári előadásában a következő áll: „Azt a feladatot tűztem
magam elé, hogy megalkossam a többszörösen kiterjedt nagyságok elméletét,
a nagyságok általános fogalmainak felhasználásával. Ebből következni fog,
hogy egy többszörösen kiterjedt nagyság képes különböző metrikus relációk
megvalósítására, következésképpen a tér csupán speciális esete a háromszorosan
kiterjedt nagyságoknak. Ebből azonban szükségszerűen következik az, hogy
a geometria állításai nem vezethetők le a nagyság általános fogalmaiból,
és hogy azok a tulajdonságok, amelyek a teret megkülönböztetik más elképzelhető
háromszorosan kiterjedt nagyságoktól, csakis tapasztalat útján igazolhatók.”
A tapasztalat szerepét a geometria és a valóság kapcsolatában még jobban
hangsúlyozta Helmholz. A Berlinben, 1810-ben alapított Frigyes Vilmos Egyetem
(a mai Humboldt Egyetem elődje) alapítási évfordulóján tartott beszédéből
vettük az alábbi idézetet.
„Ha a geometriát a tapasztalati tényekre akarjuk alapozni, ahol annak
értéke mindig a fizikai megfelelőség, csakis annak a tudománynak az állításait
alkalmazhatjuk, amelyet én fizikai geometriának neveztem. Mindenki számára,
aki az axiómákat a tapasztalatból következteti, mostanáig a mi geometriánk
valóban fizikai geometria volt”.
Kicsit odébb, Kantot bírálva, azt írja, hogy a geometria axiómáiban
lefektetett állításokat a tényleges világ viszonyaira csak azt követően
alkalmazhatjuk, ha azok érvényességét experimentálisan ellenőriztük és
megállapítottuk.
Lobacsevszkij próbálkozott azzal, hogy csillagászati mérések révén bizonyítékokat
szerezzen az új geometria mellett, de nem járt eredménnyel. Egy geometria
érvényességét persze nem lehet kísérletileg igazolni, legfeljebb cáfolni.
Elterjedt nézet (pl. Born, 1965), hogy Gauss három Hannover környéki hegycsúcs,
a Brocken, a Hohen Hagen és az Inselberg háromszögének szögeit megmérve
meg akarta tudni, hogy ezek összege 180°, vagy kevesebb, és hogy
az eredmény (a hibahatáron belül) az volt, hogy az összeg 180°.
E hegycsúcsok mindössze 107, 69, illetve 85 kilométer távolságra vannak
egymástól, így nem lenne meglepő az eredmény. Szénássy Barna (1977/1980)
azonban fényt derít arra, hogy Gauss nem csupán egy háromszöggel kapcsolatban
végzett méréseket, hanem egész méréssorozatot végzett, de nem abból a célból,
hogy eldöntse, a tér euklideszi, vagy nem. Gauss 1816-ban megbízást kapott
a hannoveri kormánytól az ország feltérképezésére, amit 1841-ig el is végzett.
Az említett háromszögből kiindulva egymás utáni háromszögeket konstruált,
melyek háromszögelési pontrendszer gyanánt szolgáltak. A méréseket a legkisebb
négyzetek módszerével kiegyenlítették, és így a másodpercek ezredrésze
nagyságrendű pontossággal kapták meg az eredményeket. Gauss nyilván nem
gondolhatta, hogy ilyen kis háromszög esetén a mérések kimutathatnak eltérést
a 180° szögösszegtől. Másfelől, a legkisebb négyzetek módszere (bár
felfogható bármilyen geometriától független numerikus eljárás gyanánt)
az euklideszi geometriával van igen jó összhangban, amit Gauss nyilván
tudott, és nem valószínű, hogy ezt a módszert alkalmazta volna, ha célja
a geometriák kísérleti ellenőrzése lett volna.
A legkisebb négyzetek módszerét Gauss egyik legjelentősebb tudományos
eredményének tartotta, emiatt prioritási vitája is támadt a kor másik nagy
matematikusával, Legendre-ral.
A fentiekhez még hozzátehetjük, hogy a legutóbbi, forgalomból már kivont
10 márkás bankjegyet Gauss emlékének szentelték. A bankjegy egyik oldalán
Gauss képe van, mellette az ún. Gauss-görbe és Göttingen látképe, a másik
oldalán pedig a szögek mérésére szolgáló szektáns, valamint a Gauss által
megalkotott térkép vázlata látható.
Jóllehet Gauss célja más volt a méréseivel, azért megállapíthatta, hogy
nem tapasztalt eltérést az euklideszi geometriától. Ezt ugyanis filozófusok
bírálták, mondván, ha a mérés eredményeként eltérést tapasztaltak volna,
ez akkor sem bizonyította volna az euklideszi geometria érvénytelenségét
(mint ahogy a hibahatáron belüli egyezés sem bizonyította annak érvényességét),
mert az eredmény lehet egy még ismeretlen fényelhajlás következménye.
A bírálók rátapintottak a lényegre. Einstein speciális relativitáselmélete
1905-ben, általános relativitáselmélete pedig 1916-ban látott napvilágot.
Az utóbbi erősen támaszkodik a nemeuklideszi geometriára, annak Riemann
által megfogalmazott változatára. Einstein elméletei azonban nem épülnek
rá a tér ilyen vagy olyan geometriájára, hanem elvetik a tér és az idő
különálló voltát és a „téridő” új fogalmából indulnak ki. Bár a relativitáselmélet
is a tudomány forradalmát jelentette, felfedezőjének elismerést és világhírt
hozott, nem pedig mellőzést. Ezt elsősorban azáltal sikerült elnyernie,
hogy egy tapasztalati tény az elméletet fényesen igazolta.
Az általános relativitáselmélet a gravitációt a tér görbületével azonosítja,
és ennek egyik megnyilvánulása, hogy nagy tömeg közelében a fény az euklideszi
egyeneshez képest elhajlik. Hogyan lehet ezt kísérletileg igazolni, vetődött
fel a kérdés, lehetőleg oly módon, hogy ne csak a jelenség általában igazolódjék
be, hanem egyezés mutatkozzék a relativitáselmélet által számított és a
tapasztalt értékek között?
A megoldást a Merkúr bolygó mozgásának a vizsgálata szolgáltatta. Csillagászok
régóta észlelték, hogy a bolygó a várt helynél kissé odébb mutatkozik.
Felvetődött, hogy a jelenség oka a fény euklideszi egyeneshez képest való
gravitációs elhajlása. Ezt oly módon gondolták ellenőrizni, hogy megvizsgálták,
lehet-e látni a Merkúrt egy olyan pillanatban, amikor a számítások szerint
tudjuk, hogy az, hozzánk képest, a Nap mögött helyezkedik el (1. ábra).
Erre a vizsgálatra természetesen csak napfogyatkozáskor kerülhet sor.
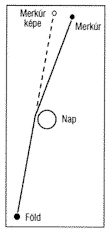
1. ábra. A Merkúrról érkező fény
elhajlása a Nap közelében
Eddington angol csillagász 1919-ben két expedíciót szervezett, az egyik
Afrika nyugati partjainál, a másik Brazília északi részén végzett megfigyeléseket,
május 29-én. E két helyen ekkor teljesültek a fent említett feltételek.
Fényképfelvételeket készítettek, és azok kiértékelése után az Einstein
elméletén alapult számítások fényesen beigazolódtak. A Merkúr sajátos pályája
miatt ez volt az egyetlen, ezekre a kísérletekre és számításokra alkalmas
bolygó.
Az első világháború befejezése után a társadalom ki volt éhezve a kultúrára,
a magasabb rendű emberi értékeket képviselő tudományos ismeretekre. Einstein
sikere mindent elsöprő volt, az újságok címlapjaira került a neve, ekkor
lett világhírű.
Einstein relativitáselmélete óta sok egyéb fizikai elmélet született,
mely fizikai terünkkel kapcsolatos. A legújabb szenzáció az, hogy bár „lokális
méretekben” a térnek görbülete van, kozmikus méretekben azonban a tér mégis,
a hibahatáron belül, euklideszinek mutatkozik!? Ez Szalay Sándornak, a
Johns Hopkins Egyetem professzorának személyes közlése. Szalay és Gray
(2001) beszámol arról, hogy az interneten hamarosan elkészül egy „virtuális
obszervatórium”, mely lehetővé teszi számítógép előtt ülve az égitestek
megfigyelését. Az ennek kapcsán épülő adatbankban eddig elhelyezett adatok
alapján jutottak erre a következtetésre. Erről részletes publikáció a 2002.
évben várható.
Mikor szerzett tudomást Bolyai Jánosról és művének nagyságáról a hivatalos
magyar tudomány? Kilenc évvel Bolyai János halála után, 1869-ben, báró
Eötvös József, aki akkor a Magyar Tudományos Akadémia elnöke és kultuszminiszter
is volt, levelet kapott Olaszországból. A levelet Baldassare Boncompagni
herceg (1821–1894), tudománytörténész és annak mecénása írta. Közölte Eötvössel,
hogy Bolyai János és Farkas életrajzát, valamint az Appendixet olasz nyelvre
lefordították, külön postával küldik Eötvösnek, és hogy az Appendixben
foglaltakat a római tudósok a XIX. század legnagyobb matematikai alkotásának
tartják. Eötvös nem tudta, hogy örüljön, vagy piruljon, írta ezt követően
fiának.
A levél megírásának hátterében Hoüel állt, aki ezen az úton próbálta
elérni, hogy a Bolyaiakkal kapcsolatos tudakozódó leveleire Marosvásárhelyről
választ kapjon. Hoüel meg volt döbbenve a magyarok nemtörődömsége miatt.
Egyik levelében azt írja, hogy „fájdalommal látom, hogy Magyarország milyen
kevésre értékeli saját tudományos érdemeit…”
Eötvös József átérezte a Bolyaiak ügyének fontosságát, és pártfogásába
vette azt. A Bolyai-hagyatékot tartalmazó csomagot azonban az Akadémia
már 1868-ban Pestre hozatta, miután Hunyady Jenő matematikus akadémikus
már bejelentést tett a Bolyai János műve iránti külföldi érdeklődésről.
A csomag letétetett az Akadémia Levéltárába. Negyedszázadig ott volt, egy
bizottság próbálta az anyagban szunnyadó új tudományos eredményeket felfedezni,
sikertelenül. Mindamellett Schmidt Ferenc ez idő alatt fedezte fel a papírok
között Bolyai János 1823. november 3-i, apjához írt levelét (… semmiből
egy ujj, más világot teremtettem). Később azonban, már Marosvásárhelyen,
felfedezték a matematikai tartalmú kéziratok között az Appendix után írt
művek egy részét. Ezek a következők: Responsio, a lipcsei Jablonowski Társasághoz
benyújtott pályázat anyaga; Kiegészítések (az Appendixhez); A (hiperbolikus
geometriában a) tetraéder köbösítése (köbtartalmának meghatározása); Ellentmondás-mentességi
vizsgálatok; Észrevételek (Lobacsevszkij művével kapcsolatban); Raumlehre.
Benkő Samu kolozsvári történészprofesszor volt az, aki Abafáy Gusztávnak
a segítségével a hátrahagyott Bolyai-kéziratokat rendszerezte. Tizenhat
év munkájával sorba állította és dossziékban elhelyezte a tizennégyezer
oldalnyi kéziratot. Ebben segítségére voltak Bolyai János „őrszavai”. Bolyai
János több lap alján az utolsó szót a következő lap tetején megismételte,
ezeket őrszavaknak nevezte. Benkő Samu a kéziratokat elolvasta és 1968-ban
publikálta a nem matematikai jellegűekről szóló könyvét Bolyai János vallomásai
címmel. A háromezer oldalnyi matematikai kéziratot Kiss Elemér marosvásárhelyi
professzor olvasta végig az 1990-es években és beszámolóját az 1999-ben
megjelent könyvében és cikkében tette közzé. A kéziratokban olyan jelentős
matematikai eredményeket fedezett fel, melyek abban az időben újak voltak.
Ilyen pl. az a számelméleti tétel, melyet Jeans harmincnyolc évvel Bolyai
János halála után publikált és ma tankönyvanyag. Mindkét professzor hatalmas
és rendkívül értékes munkát végzett. Bolyai János kéziratainak egy részét
színlapokra, borítékok hátlapjára írta, így nemcsak azok értelmezése, hanem
puszta elolvasása is óriási munka volt. Jelenleg folyamatban van Bolyai
János teljes kéziratanyagának a publikálása, Benkő Samu gondozásában.
A marosvásárhelyi gyűjteményen kívül van egy Bolyai-gyűjtemény a Magyar
Tudományos Akadémia Könyvtárában. Ez jelentős részben Szabó Péter adománya
révén keletkezett. Szabó Péter apja, Szabó Sámuel, marosvásárhelyi tanár
volt, aki tanulmányozta a Bolyai-kéziratokat, ezek egy részét hazavitte,
nála felejtődött és halála után a hagyatékából került elő. Az anyagot Szabó
Péter átadta az Akadémiának, de maga is sok kéziratot, levelet gyűjtött
a Bolyaiakkal kapcsolatban. A gyűjteményt Fráterné (1968) rendszerezte
és katalogizálta, nemrég Vekerdi (2001) írt róla érdekes cikket. A Bolyaiak
felfedezésének korábbi történetéről Szénássy Barna (1977/1980) írt összefoglaló
cikket.
A Bolyaiak, különösen János és műve tisztelete egyre növekedett. 1897-ben
az Appendix magyar fordításban is megjelent (Rados Ignác), ugyanebben az
évben megjelent Bedőházy (Bolyai Farkas utódja a Marosvásárhelyi Kollégiumban)
könyve „A két Bolyai” címmel, 1897-ben Kőnig Gyula és Réthy Mór szerkesztésében
újból kiadták a Tentamen első kötetét, 1904-ben Kürschák József, Réthy
Mór és Tőttösy Béla szerkesztésében a második kötetét. Bolyai János Appendixe
a második kötet végére került. Bolyai János születésének 100. évfordulója
alkalmából emlékülést rendeztek Kolozsvárott. A Mathematikai és Physikai
Lapokban 1903-ban több cikk jelent meg Bolyai Jánossal és geometriájával
kapcsolatban (Beke Manó, Réthy Mór, Szabó Péter, Schlesinger Lajos tollából,
az utóbbi a kolozsvári ünnepség vezérszónoka volt). Az Akadémia 1902-ben
Bolyai-díjat alapított, amit 1905-ben Poincaré, 1910-ben pedig Hilbert
kapott meg. Mindketten fontos eredményeket értek el a geometria alapjaival
és közelebbről, a hiperbolikus geometriával kapcsolatban is. (Poincaré
ekkor szerzett tudomást arról, hogy Bolyai János magyar volt és nem bolgár,
ahogyan azt az 1905-ben megjelent La valeur de la science című könyvében
írta.)
Bolyai János születésének 150. évfordulója alkalmából Budapesten, a
Magyar Tudományos Akadémián rendeztek emlékülést. Anyagát a Matematikai
és Fizikai Tudományok Osztályának Közleményeiben közölték (szerzők: Kárteszi,
Varga, Szász, Alexits, Kalmár, Hadamard). A 175. éves évforduló alkalmából
újból az Akadémián volt szerényebb emlékülés, az előadások (Császár, Bretter,
Sarlóska, Gazda, Lambrecht, Molnár) anyaga a Természet Világában jelent
meg. Az eddigi utolsó emlékülést a 190. évfordulóra szintén az Akadémia
szervezte. A 200. évfordulót nagy nemzetközi konferenciával Budapesten
ünnepeljük, az Akadémia, a Bolyai János Matematikai Társulat, az Eötvös
Loránd Fizikai Társaság, az ELTE, a Debreceni Egyetem, a Szegedi Egyetem,
a kolozsvári Babeş-Bolyai Egyetem,
az erdélyi Sapientia Egyetem, az MTA Matematikai Kutatóintézete és az MTA
SZTAKI szervezésében.
Bolyai és Lobacsevszkij kidolgozta, és szisztematikusan felépítette
a hiperbolikus geometriát, mely egyben az első nemeuklideszi geometria
volt (ha eltekintünk korábbi, befejezetlen kísérletektől). E két nagy tudós
azonban még nem bizonyította be az új geometria ellentmondás-mentességét.
Az ellentmondás-mentességet oly módon bizonyítjuk, hogy megadunk egy
modellt, vagyis a matematikai objektumok egy összességét, egymáshoz való
kapcsolatukkal, oly módon, hogy ezek az axiómákat, adott esetben a hiperbolikus
geometria axiómáit teljesítik. Ha ugyanis van legalább egy realizációja
az axiómarendszernek, akkor az nem lehet ellentmondásos.
Elsőként az olasz Beltrami (1868) adott modellt a hiperbolikus geometriára.
Ebben felhasználta Minding (1838) munkáját és a Riemann-geometria apparátusát.
A modell az ún. pszeudoszféra, mely a traktrix forgásfelülete. A traktrix
görbét az jellemzi, hogy bármely pontjához húzott érintőnek az érintési
pont és a függőleges tengely közötti szakasza állandó hosszúságú (2.
ábra).
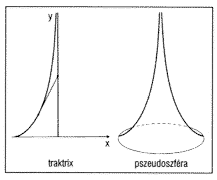
2. ábra. A traktrix és forgásfelülete
A traktrixot Huygens kutyagörbének nevezte, mert ha a vonakodó kutyát
pórázon húzzuk az y tengely mentén, akkor a kutya a traktrix mentén
mozog. A pszeudoszféra felületén az „egyenest” az jellemzi, hogy bármely
két pontja között a legrövidebb utat valósítja meg.
Poincaré modelljei ennél is egyszerűbbek. Az egyikben a pontok a perem
nélküli (nyílt) körlap pontjai, az egyenesek pedig azok a (nyílt) körlapon
belüli körívek, amelyek a peremmel merőlegesen találkoznak, továbbá a kör
középpontján áthaladó euklideszi egyenesek. Poincaré másik modellje a nyílt
félsík, az x tengely fölötti rész. Ebben a modellben az egyenes
vagy olyan félkör, mely az x tengelylyel két pontban, merőlegesen
találkozik, vagy olyan euklideszi egyenes, mely az x tengelyre merőleges
(3.
ábra).
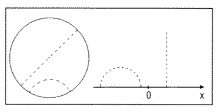
3. ábra. Poincaré körlap és félsík modellje „egyenesekkel”
A hiperbolikus geometriának sok alkalmazása van a matematikában és más
tudományokban egyaránt. A matematikán belül a komplex függvénytanban nélkülözhetetlen
eszköz az ún. Riemann-féle felületek tárgyalásában. Továbbfejlesztett változatai
megjelennek a diszkrét geometriában, a topológiában, a csoportelméletben
stb. Ami a fizikai alkalmazásokat illeti, legfontosabb a közvetett alkalmazása,
megalkotása utat nyitott a Riemann-féle és más geometriák felé, melyek
az általános relativitáselmélet matematikai alapjait szolgáltatják. Ám
közvetlenül is alkalmazzák a hiperbolikus geometriát a relativitáselméletben
(l. pl. Ungar cikkét, 1997). További alkalmazást találunk a statisztikus
fizikában. Újabban az interneten az elágazó fák képernyőn való elrendezését
a hiperbolikus geometria körlapmodelljére támaszkodva alkotják meg (pl.
Gunn, 1993).
A hiperbolikus geometria világa nemcsak a tudósokra volt és van nagy
hatással, hanem a művészekre is. Közöttük elsőként Eschert kell említenünk.
Escher több grafikája, metszete foglalkozik olyan alakzatokkal, melyek
egy körön belül helyezkednek el, és egyre kisebb példányaik a kör pereméhez
közelednek. A perem közvetlen közelébe Escher kis köröcskéket helyezett
el, melyek természetüknél fogva nem töltötték ki a körlapot. Miután azonban
a művész tanulmányozta a híres kanadai geométer, H. S. MacDonald Coxeter
hiperbolikus geometriai ábráit, és a tudóssal személyesen is megismerkedve
annak képeivel kapcsolatos tanácsait elfogadta, megalkotta a csodálatos
„circle limit” metszeteit. Ezeken a hiperbolikus geometria Poincaré-féle
körlap modelljének „egyenesei” (euklideszi értelemben körívei) egyre kisebbé
válva konvergálnak a peremhez (l. Escher 1989, 1992, 1995). A 4. ábrán
reprodukáljuk Coxeter (1998) ábráját, az 5. ábrán pedig Escher Circle
Limit III. című metszetét. Coxeter (1979) egy cikkben visszatért erre a
metszetre és feltárta annak kapcsolatát a nemeuklideszi geometriával.
Egy másik, hiperbolikus geometriával kapcsolatos műalkotás
a berlini Conrad Pelthier munkája. Ennek alapjául Reynolds (1993) cikke
szolgált, melyben a szerző a hiperbolikus geometria egy hiperboloidon megvalósított
modelljét írja le. A kép Stillwell (1996) könyvének borítólapján is látható.
Végül megemlítjük, hogy az Amerikai Egyesült Államok Berkeley (Kalifornia)
egyetemén működő Mathematical Research Institute (MSRI) intézete nemrég
egy matematikai szobrot készíttetett, melyet annak udvarán állítottak fel.
A szobor Felix Klein ún. kvartikus görbéjét ábrázolja és címe: „The eightfold
way”. A szobor talapzatán a hiperbolikus geometria körlap modelljét idéző
színes cserépmozaikot rakattak, mégpedig a magyar Biczó Lajossal, arra
emlékezve, hogy a hiperbolikus geometria egyik felfedezője magyar ember
volt. A szoborról egész könyvet írtak, Lévy (2001) szerkesztésében.
Az axiomatikus gondolkodásról
A matematika történetében a nemeuklideszi geometria lett az első olyan
ellentmondásmentes, zárt, logikai rendszer, mely nincs közvetlen kapcsolatban
a valósággal. Megalkotása a fizikai valóságból indult ki, ám önálló matematikai
elméletté vált. Ezzel nem az következett be, hogy alkalmazhatatlanná vált
volna, hanem éppen ellenkezőleg, lehetővé vált, hogy matematikusok, fizikusok,
számítástechnikusok és mások felhasználják, alkalmazzák a problémák nagy
sokaságára.
A nemeuklideszi geometria nem az egyetlen önálló matematikai elmélet,
mely Bolyai idejében keletkezett. A XIX. század közepén Angliában és Írországban
megszületett az absztrakt algebra, vagy ahogyan abban az időben nevezték,
szimbolikus algebra. Már a század elején a matematikusok szabadon végeztek
műveleteket valós és komplex számokkal, anélkül hogy akármelyik, kiváltképpen
pedig a komplex számok, rendelkezett volna mai értelemben vett egzakt matematikai
megalapozással. Ez szükségessé tette, hogy a műveleti szabályok (asszociativitás,
kommutativitás stb.) világos, áttekinthető rendszerbe legyenek foglalva.
Egyidejűleg az is felvetődött, hogy a műveleteket kiterjesszék, pl. lehetséges
legyen egy pozitív valós számnak valós hatványra emelése. Szimbólumokkal
számoltak, a játékszabályok betartásával. Az is felvetődött, hogy ezeket
a szabályokat elvontan tekintsék, ne csupán számokra vonatkoztassák.
A szimbólumok szerepét a matematikai gondolkodásban már Kant is tárgyalta
műveiben. Lambert az euklideszi XI. axiómát a többitől tisztán szimbolikusan
akarta levezetni (1786, § 11).
George Peacock (1791–1858) Cambridge matematikusa, később az Ely katedrális
dékánja volt az első Angliában, aki a matematikai manipulációk megalapozásának
a szükségességét felvetette. Nem szorítkozott az algebrára, a problémát
kiterjesztette a differenciálszámításra is. Az algebránál maradva Duncan
Gregory (1813–1844) a következő jelentős személyiség a szimbolikus algebra
létrehozásában. Álláspontját egy 1840-ből származó művében az alábbi módon
jellemzi: „A szimbolikus algebrát annak fényében tekintem, hogy az a műveletek
kombinációinak a tudománya, nem annak természete által, hogy azok mik és
mit eredményeznek, hanem azok által a törvények által, amiknek engedelmeskednek”.
Az algebrát tehát eltávolították attól, amire korábban használták, a pozitív
valós számokkal való műveletektől, pontosabban szólva, kiterjesztették
a hatókörét.
A következő fontos lépést De Morgan (1806–1871) tette meg. Ő volt az
első, aki az új algebrának a logikában való alkalmazását felvetette. Tőle
származnak azok a szimbolikus logikai operációk, amelyeket De Morgan-törvényeknek
nevezünk.
Az ír származású Hamilton (1805–1865) algebrai vonatkozású eredményei
körül a komplex számok egzakt megalapozását és a kvaterniók fogalmának
a megalkotását, elméletének a kiépítését kell megemlítenünk. (A kvaterniókról
szóló művét megküldte Gaussnak és hasonló választ kapott, mint Bolyai János
az Appendixre.)
George Boole (1815–1864) munkássága és elsősorban 1854-ben közreadott
The Laws of Thought című könyve a következő, melyet a felsorolásban megemlítünk.
A nevéhez fűződő algebrát szinte mindenki ismeri, alkalmazása a matematikában,
a logikában, az áramkörök elméletében stb. igen jól ismert.
Arthur Cayley (1821–1895) és James Joseph Sylvester (1814–1897) elsősorban
a mátrixelmélet és a csoportelmélet megalkotásával vett részt a brit algebrai
iskola tevékenységében.
Absztrakt geometria, absztrakt algebra stb., a matematika tehát most
már nem szól semmi konkrétumról, csak elvont struktúrákról? Ezzé vált volna
a matematika súlyos problémák megoldása után? Csak absztrakt matematika
van és a valósághoz nincs már semmi köze? Nem erről van szó. A matematika
módszere azonban abban áll, hogy a valóságos objektumokat matematikai objektumokkal
helyettesítjük, modellt alkotunk, és azon belül oldjuk meg a matematikai
problémákat. A valósághoz azonban vissza kell térnünk. Eredményeinket alkalmaznunk
kell, annál inkább, mert az új gondolatok, modellek, struktúrák keletkezésének
ez a legfőbb forrása. Persze vannak félresiklások, ezek körül nagy vita
folyik. Érdekes vitacikk például Thom (1971) munkája, melyben a valóságtól
elszakadt matematikai alkotásokat és a túlságosan absztrakt oktatási módot
bírálja.
A XIX. század közepén nem csak a matematikában erősödött fel az axiomatikus
módszer alkalmazása. Az axiomatizálási láz más tudományokra is átterjedt.
Az axiomatizálás a fizikában persze nem számított új dolognak, most azonban,
meglepő módon, a mérnökök is egzakt alapokra akartak helyezni egy-egy műszaki
tudományt azok axiomatizálása révén. Ennek az irányzatnak két jeles képviselője
a német Ferdinand Redtenbacher (1809–1863) és a svájci Franz Reuleaux (1829–1905).
A változókat és a lehetséges mozgásokat rendszerezték, meghatározták egymáshoz
való viszonyukat és a mechanizmusokkal kapcsolatban tételeket is bizonyítottak.
Ennek az elméletnek a gyakorlati hasznát abban az időben ugyan megkérdőjelezték,
ám alkotóikat segítette új mechanizmusok konstrukciójában (l. S. Brentjes,
1882).
Az axiomatikus gondolkodásnak vannak korlátai is. Az egyiket ezek közül
Gödel (1931) fogalmazta meg híres tételében. Gödel bebizonyította, hogy
minden, elég általános feltételeknek eleget tevő axiómarendszeren belül
megfogalmazható olyan probléma, mely sem igenlően, sem tagadólag nem válaszolható
meg. Erre Eukleidész V. posztulátumának problémája a legklasszikusabb példa.
Más természetű korlátot jelent az, hogy a matematikusok hajlamosak lettek
arra, hogy csak axiómarendszerek kínálta problémákkal foglalkozzanak és
megfeledkezzenek az elméleteknek a valósággal való kapcsolatáról. Igen
érdekes gondolatokat olvashatunk erről Von Mises (1957) könyvében. E kérdéskör
kifejtésére egy másik cikkben térünk majd vissza.
Az axiomatikus gondolkodás és feladatmegoldás a tudományt alkalmazók
mindennapi kenyerévé vált. Amikor egy probléma megoldásához hozzáfogunk,
összegyűjtjük változóinkat, állandóinkat, meghatározzuk ezek kapcsolatát,
és ha matematikai jellegű problémáról van szó, akkor egy eljárást, algoritmust
is megalkotunk, vagy egyszerűen csak felhasználunk. A feladatok megoldása
azonban egy ember-gép rendszerrel történik, a gép ma elektronikus, digitális
számítógépet jelent. A legegyszerűbb gép, melyet ősidők óta felhasználnak,
a körző és a vonalzó. Ezek tulajdonképpen analóg gépek. Amikor egy geométer
valamilyen geometriai objektumot megszerkeszt, akkor azt az ember-gép rendszert
használja fel, amelyben a gép a körző és a vonalzó. Az abakusz, majd később
Pascal, Leibniz, Babbage, Zuse számítógépei (l. Korte, 1981) egyre bonyolultabb
feladatok megoldását tették lehetővé egyre hatékonyabban. Ma már az 1946-ban
megszületett ENIAC (Electronic Numerical Integrator and Computer) első
elektronikus számítógép nagy teljesítményű utódait használjuk feladataink
megoldására.
A modern feladatmegoldásnak ez a technikája ma nagyon hatékonyan működik.
Ebben, mint említettük, alapvetően fontos momentum az axiomatikus gondolkodás,
ugyanis minden egyes feladatot egy-egy axiómarendszerrel írunk le. Az axiomatikus
gondolkodás széles körű elterjedése egyike azoknak, amiket Bolyai János
forradalma eredményezett.
Bolyai János munkássága tehát nem csupán a geometriában, a matematika
egészében, a filozófiában és a kultúrtörténetben hozott újat, hanem utat
nyitott a feladatmegoldás új szemléletmódja számára is.
Irodalom
[1] Alexits Gy. (1952). Bolyai János. Matematikai Lapok 3, 107–110.
[2] Alexits Gy. (1953). Bolyai János élete és munkássága. MTA Mat. Fiz.
Tud. Oszt. Közl. 3, 131–150.
[3] Alexits Gy. (1977). Bolyai János világa. Akadémiai Kiadó, Budapest,
1977.
[4] Alexits Gy. (1977/1980). Bolyai János világa. Matematikai Lapok
28, 1–9
[5] Anderson, J. W. (1999). Hyperbolic geometry. Springer Verlag, London.
[6] Ács T. (1997). Bolyai János a bécsi császári és királyi mérnökakadémián
1818–1823. Bolyai János Katonai Műszaki Főiskola, Budapest.
[7] Ács T. (1998). Egy ismeretlen akadémiai pályázat sorsa. Hadtörténeti
Közlemények 111, 284–291.
[8] Barndorff-Nielsen, O. (1978). Hyperbolic distributions and distributions
on hyperbolae. Scand. J. Statist, 5, 151–157.
[9] Beke M. (1903). A Bolyai-féle trigonometria. Mathematikai és Physikai
Lapok 12, 30–49.
[10] Bell, E. T. (1972). The Development of Mathematics. Dover Publications
Inc., New York.
[11] Bell, E. T. (1986). Men of Mathematics. Simon and Schuster, New
York.
[12] Beltrami, E. (1868). Saggio di interpretazione della geometria
non-euclidea. Giornate di Matematiche VI., 284–312.
[13] Beltrami, E. (1868). Teoria fondamentale degli spazii di curvatura
costante. Ann. Mat. pura appl. Ser. II, 232–255.
[14] Benkő S. (1968). Bolyai János vallomásai. Irodalmi Könyvkiadó,
Bukarest. Második kiadás: Kritérion Könyvkiadó, Bukarest, 1972.
[15] Benkő S. (1971). Sorsformáló értelem. Művelődéstörténeti dolgozatok.
Kritérion Könyvkiadó, Bukarest.
[16] Benkő S. (1978). Apa és fiú (Bolyai tanulmányok). Magvető Könyvkiadó,
Budapest.
[17] Benkő S. (1979). Haladás és megmaradás. Művelődéstörténeti tanulmányok.
Szépirodalmi Könyvkiadó, Budapest.
[18] Bolyai F. (1830). Az arithmetica eleje. Marosvásárhely.
[19] Bolyai Farkas (1832–1833). Tentamen juventutem studiosam matheseos
purae, elementaris ac sublimioris, methodo intuitiva evidenciaque huic
propria, introducendi. Cum appendici triplici. I., II. Marosvásárhely.
[20] Bolyai Farkas (1897, 1904). Tentamen (második kiadás, szerkesztők:
Kőnig Gy. és Réthy M. első kötet, Kürschák J., Réthy M. és Tőttössy B.,
második kötet). Magyar Tudományos Akadémia.
[21] A Bolyai–Gauss-levelezés (2001). Válogatta és szerkesztette Nagy
F. Better, Püski, Budapest.
[22] Bolyai Joannes (1831). Appendix prima scientia spatii, a veritate
aut falsitate axiomatis XI-mi Euclidei (a priori haud unquam decidenda)
independens: atque ad casum falsitatis quadratura circuli geometrica. Marosvásárhely.
[23] Bolyai Joannes (1832). Appendix Stientiam Spatii absolute veram
exhibens: a veritate aut falsitate Axiomatis XI. Euclidei (a priori haud
unquam decidenda) independentem; adjecta ad casum falsitatis, quadratura
circuli geometrica. In: Bolyai F., Tentamen, Tom. I. Marosvásárhely.
[24] Bolyai János (1868). La science absolue de l’espace… (latinból
fordította Hoüel. Bordeaux Mem. 5, 207–248.
[25] Bolyai János (1868). Sulla scienza della spazio assolutamente vera…
(latinból fordította Battaglini). Giorn. Mat. 6, 97–116.
[26] Bolyai János (1891). The science of absolute space… (fordította
G. B. Halsted). Austin, Texas. További kiadások 1892, 1894, 1896.
[27] Bolyai János kéziratos hagyatéka. Bolyai–Teleki Könyvtár. Marosvásárhely,
[28] Bolyai-levelek (1975). Válogatta, a bevezető tanulmányt írta és
a jegyzeteket összeállította Benkő Samu. Kritérion Könyvkiadó, Bukarest.
[29] Bolyai János (1977). Appendix, a tér tudománya (szerk. Kárteszi
Ferenc). Akadémiai Kiadó, Budapest.
[30] Bolyai Jánosra emlékezünk! Születésének 175. évfordulóján (szerk.
Staar Gyula). Tudományos Ismeretterjesztő Társulat budapesti szervezete,
Budapest, 1978.
[31] Bolyai (2001). Biográfia, bibliotéka, bibliográfia (szerk. Nagy
F.). Better, Püski, Budapest.
[32] Bonola, R. (1911). Non-Euclidean Geometry. Dover, New York.
[33] Boole, G. (1854). An Investigation of the Laws of Thought on which
are Founded the Mathematical Theories of Logic and Probabilities. Macmillan,
Cambridge.
[34] Born, M. (1965). Einstein’s Theory of Relativity. Dover, New York.
[35] Bos, H. J. M. (2001). Redifining geometrical exactness. Descartes
transformation of the early modern concept of construction. Springer, New
York.
[36] Boyer, C. B. (1991). A History of Mathematics, (második kiadás).
Wiley, New York.
[37] Brentjes, S. (1982). Relations between mathematics and engineering
in the 19th century in Germany (kézirat).
[38] Bretter Gy. (1978). A felőrlődés logikája. Természet Világa 109,
92–93.
[39] Briefwechsel zwischen Carl Friedrich Gauss und Christian Ludwig
Gerling (1927). Clemens Schaeffer, Berlin.
[40] Briefwechsel zwischen C. F. Gauss-Friedrich Wilhelm Bessel (1975).
Georg Olms Verlag, Hildesheim, New York.
[41] Briefwechsel zwischen C. F. Gauss und H. C. Schumacher, 1–3 (1975).
Georg Olms Verlag, Hildesheim, New York.
[42] Burton, D. M. (1985). The History of Mathematics. An Introduction.
Allyn and Bacon Inc. Boston, London.
[43] Cajori, F. (1991). A History of Mathematics. Chelsea Publ. Co.,
New York.
[44] Caygill, H. (2000). A Kant Dictionary. Blackwell.
[45] Cayley, A. (1854). On the Theory of Groups. Philosophical Magazine
7, 40–47.
[46] Coxeter, H. S. M. (1977). Gauss as a Geometer. Historia Mathematica
4, 379–396.
[47] Coxeter, H. S. M. (1979). The non-Euclidean symmetry of Escher’s
picture „Circle Limit III.” Leonardo 12 (1979), 19–25.
[48] Coxeter, H. S. M. (1998). Non-Euclidean geometry, 6th
ed., Mathematical Association of America, Washington, DC.
[49] Császár Á. (1978). Bolyai János és Gauss. Természet Világa 109,
89–92.
[50] Dávid L. (1959). In memoriam Wolfgang Bolyai. MTA Mat. Fiz. Tud.
Oszt. Közl. 9, 215–236.
[51] Dávid L. (1979). A két Bolyai élete és munkássága. Második, bővített
kiadás. Gondolat, Budapest.
[52] Deé Nagy Anikó (2000). A két Bolyai könyvtára. Erdélyi Múzeum 1–2.
szám, 19–45.
[53] Dunnington, G. W. (1955). Gauss: titan of science. Hafner, New
York.
[54] Escher, M. C. (1989). Escher on Escher: exploring the infinite.
Harry N. Abrams, New York. With contribution by J. W. Vermeulen; hollandból
fordította Karin Ford.
[55] Escher, M. C. (1992). The graphic work: introduced and explained
by the artist, Benedikt Taschen Verlag.
[56] Escher, M. C. (1995). The M. C. Escher sticker book. Harry N. Abrams,
New York.
[56a] Eukleidész (1983). Elemek. Gondolat, Budapest.
[57] Ewald, W. (1999). From Kant to Hilbert. A Source Book in the Foundations
of Mathematics Vols. I, II. Clarendon Press, Oxford.
[58] Fowler, D. (1999). The Mathematics of Plato’s Academy. A new reconstruction.
(második kiadás). Clarendon Press, Oxford.
[59] Fráter Jánosné (1968). A Bolyai-gyűjtemény. Magyar Tudományos Akadémia
Könyvtára (K22–K30).
[60] Frege, G. (1884). Die Grundlagen der Arithmetik, eine logisch-mathematische
Untersuchung über den Begriff der Zahl. Koebner, Breslau. (Angol fordítása:
The Foundations of Arithmetic, A Logico-Mathemathical Enquiry into the
Concept of Number. Basil Blackwell, Oxford, 1950, átdolg. 2. kiadás 1953;
fordító: John Langshaw).
[61] Gauss, C. F. (1870–1929). Werke, 1–12. kötetek, második nyomás.
Göttingen, Gotha, Leipzig, Berlin.
[62] Gödel, K. (1931). Über formal unentscheidbare Satze der Principia
Mathematica und verwandte Systeme. Monat. Math. Phys. 38, 173–198.
[63] Grabiner, J. V. (1974). Is Mathematical Truth Time-Dependent? American
Math. Monthly 81, 354–365.
[64] Grattan-Guinness, I. (1998). The Norton History of the Mathematical
Sciences. Norton and Co. New York.
[65] Gray, J. (1979). Ideas of Space. Clarendon Press, Oxford.
[66] Gray, J. (1979). Non-Euclidean Geometry – A Re-Interpretation.
Historia Mathematica 6, 236–258.
[67] Greenberg, M. J. (1993). Euclidean and Non-Eucliden Geometries
(harmadik kiadás). Springer, New York.
[68] Gregory, D. F. (1840). On the nature of symbolical algebra. Transactions
of the Royal Society of Edinburgh 14, 208–216.
[69] Gunn, C. (1993). Discrete groups and visulaization of three-dimensional
manifolds. In: ACM SIGGRAPH Computer Graphics Proceedings, Annual Conference
Series, 255–262.
[70] Hadamard, J. (1953). A nem-euklideszi geometria és az axiomatikus
definíciók. MTA Mat. Fiz. Tud. Oszt. Közl. 3, 199–208.
[71] Hadamard, J. (1999). Non-Euclidean Geometry in the Theory of Automorphic
Functions (J. J. Gray and A. Shenitzer eds.). History of Math. Vol. 17,
Amer. Math. Soc., London Math. Soc.
[72] Hamilton, W. R. (1837). Theory of conjugate functions, or algebraic
couples; with a preliminary and elementary essay on algebra as the science
of pure time. Transactions of the Royal Irish Academy 17, 293–422.
[73] Hamilton, W. R. (1853). Lectures on Quaternious. Hodges and Smith,
Dublin.
[74] Hamilton, W. R. (1931–1967). The Mathematical Papers of Sir William
Hamilton (H. Halberstam and R. E. Ingram eds.). Cambridge University Press.
[75] Hankel, H. (1884). Die Entwicklung der Mathematik in den letzten
Jahrhunderten (második kiadás). Verlag und Druck von Franz Vues, Tübingen
[76] Hartshorne, R. (2000). Geometry: Euclid and Beyond. Springer, New
York.
[77] Helmholz, H. (1878). Die Thatsachen in der Wahrnehmung. Berlin.
[78] Helmholz, H. (1884). Vortrage und Reden I, II. Vieweg, Braunschweig.
[79] Hollingadale, S. (1994). Makers of Mathematics. Penguin Group,
New York.
[80] Iversen, B. (1992). Hyperbolic geometry. Cambridge University Press,
Cambridge, UK.
[81] Jelitai J. (1939). Bolyai János 1849. május 13-án kelt jelentés
tervezete. Matematikai és Természettudományi Értesítő 58, 708–715.
[82] Kaestner, A. G. (1790). Was heisst in Euclids Geometrie möglich?
Philosophisches Magazin herausgegeben von J. A. Eberhardt. Halle a. S.
[83] Kalmár L. (1953). A Bolyai–Lobacsevszkij-féle geometria hatása
az axiomatikus módszer fejlődésére. MTA Mat. Fiz. Tud. Oszt. Közl. 3, 235–242.
[84] Kant, I. (1781, 1787). Kritik der reinen Vernunft. (Első, második
kiadás.) Johann Friedrich Hartknoch, Riga.
[85] Kant, I. (1788) Kritik der praktischen Vernunft. Johann Friedrich
Hartnoch, Riga.
[86] Kant, I. (1790). Erste Einleitung in die Kritik der Urteilskraft.
L. Kant művei 5. kötet, kiadta E. Cassirer, 1922.
[87] Kárteszi F. (1953). Lobacsevszkij élete és munkássága. MTA Mat.
Fiz. Tud. Oszt. Közl. 3, 189–197.
[88] Kárteszi F. (1976). Bolyai János életműve. Matematikai Lapok 27,
59–63.
[89] Kárteszi F. (1980/1983). Az Appendix előzményei és tudományos eredményei.
Matematikai Lapok 31, 15–22.
[90] Kiss E. (1994). A „Bolyai-ládák” legújabb titkai. Természet Világa
125, 405–408.
[91] Kiss E. (1999). Matematikai kincsek Bolyai János kéziratos hagyatékából.
Akadémiai Kiadó, Budapest.
[92] Kiss E. (1999). Notes on János Bolyai’s researches in number theory.
Historia Mathematica 26, 68–76.
[93] Klein, F. (1872). Vergleichende Bertrachtungen über neuere geometrische
Forschungen (Erlanger Programm). Akademische Verlagsgesellschaft, Leipzig,
1974.
[94] Klein, F. (1873). Über die sogenannte Nicht-Euklidische Geometrie.
Math. Ann. 6, 112–145.
[95] Klein, F. (1928). Vorlesungen über Nichteuklidische Geometrie.
Springer, Berlin.
[96] Kline, M. (1990). Mathematical Thought from Ancient to Modern Times
I. II. III. Oxford University Press, Oxford, UK.
[97] Koncz J. (1887). A marosvásárhelyi Evangélikus–Református Kollégium
Könyvnyomdájának száz éves története. Marosvásárhely.
[98] Koncz J. (1896). A marosvásárhelyi Evangélikus–Református Kollégium
Története. Marosvásárhely.
[99] Kosáry D. (2001). Újjáépítés és polgárosodás 1711–1867. História/Holnap
Kiadó, Budapest.
[100] Korte, B. (1981). Zur Geschichte des maschinelles Rechnens. Bouvier
Verlag, Herbert Grundmann, Bonn.
[101] Lambert, J. H. (1786). Theorie der Parallellinien In: Engel und
Stäckel (1895).
[102] Lambrecht M. (1973). Bolyai János mint regényhős. Természet Világa
104, 504–505.
[103] Lánczos K. (1976). A geometriai térfogalom fejlődése. Gondolat,
Budapest.
[104] Legendre, A. M. (1794). Eléments de géométrie. Paris.
[105] Lévy, S. ed. (2001). The eightfold way. The beauty of Klein’s
quartic curve. Cambridge University Press, Cambridge, UK.
[106] Lobacsevszkij, N. I. (1837). Géometrie imaginaire. Journal für
de Reine Und Angewandte Mathematik 17, 295–320.
[107] Lobacsevszkij, N. I. (1840). Geometrische Untersuchungen zur Theorie
der Parallellinien. Berlin.
[108] Lobacsevszkij, N. I. (1951). Geometriai vizsgálatok a párhuzamosok
elméletének köréből (V. F. Kagan bevezetésével, magyarázataival és függelékével).
Akadémiai Kiadó, Budapest.
[109] Milnor, J. (1982). Hyperbolic geometry: The first 150 years. Bull.
(New Series) Amer. Math. Soc. 6, 9–24.
[110] Minding F. (1838). Über die Biegung krummer Flächen. J. reine
angew. Math. 18, 365–368.
[111] von Mises, R. (1981). Probability, statistics and truth. Dover,
New York.
[112] Molnár E. (1975). Bolyai János és a „tér tudománya”. Természet
Világa 106, 469–470.
[113] Nagy I. (1858). Magyarország családjai címerekkel és nemzedéki
táblákkal II. kötet. Pest.
[114] Orbán B. (1868). A Székelyföld leírása történelmi, régészeti s
népismei szempontból. Ráth Mór Bizománya. Pest.[115] Pálffy I. és Pálffy
M. (1962). Bibliographia Bolyaiana 1831–1960. A Bolyai geometria szakirodalmának
jegyzéke. Országos Széchényi Könyvtár, Budapesti Műszaki Egyetem Központi
Könyvtára.
[116] Peacock, G. (1830). A Treatise on Algebra. Deighton, Cambridge.
[117] Poincaré, H. (1960). Mathematical Creation. In: The World of Mathematics,
Vol. 4 (J. R. Newman ed.). George Allen and Unwin Ltd., London, 2041–2050.
[118] Poincaré, H. (1985). Papers on Fuchsian Functions. Springer-Verlag.
[119] Poincaré, H. (1905, 2001). La valeur de la Science. Angol fordítása:
The value of science. The Modern Library, New York.
[120] Redtenbacher, F. (1852). Prinzipien der Mechanik und des Maschinenbaus.
Mannheim.
[121] Rényi A. (1952). Bolyai János a tudomány nagy forradalmára. Matematikai
Lapok 3, 174–178.
[122] Réthy M. (1903). Bolyai János „ujj, más világának ismertetése”.
Mathematikai és Physikai Lapok 12, 1–29.
[123] Reuleaux, F. (1875). Theoretische Kinematik. Braunschweig.
[124] Reynolds, W. F. (1993). Hyperbolic Geometry on a Hyperboloid.
American Mathematical Monthly 100, 442–455.
[125] Riemann, B. (1868). Über die Hypotehesen, welche der Geometrie
zu Grunde liegen. Abhandlungen der Königlichen Gesellschaft der Wissenschaften
zu Göttingen 13, 133–152.
[126] Riemann, B. (1876). Gesammelte Mathematische Werke und Wissenschaftlicher
Nachlass (H. Weber és R. Dedekind szerk.) Teubner, Leipzig.
[127] Riemann, B. (1921). Über die Hypothesem, welche der Geometrie
zu Grunde liegen. (Új kiadásban, H. Weyl magyarázatával). Julius Springer,
Berlin.
[128] Saccheri, G. (1920). Euclides vindicatus (fordította G. B. Halsted).
Open Court, Chicago.
[129] Sarlóska E. (1965). Bolyai János – a katona. MTA Mat. Fiz. Tud.
Oszt. Közl. 15, 341–387.
[130] Sarlóska E. (1973). A 150 éves „Bolyai”. Természet Világa 104,
482–484, 507.
[131] Sarlóska E. (1973). Gondolatok Benkő Samu könyvéről. Természet
Világa 104, 504.
[132] Schlesinger L. (1903). Bolyai János. Mathematikai és Physikai
Lapok 12, 57–88.
[133] Schlesinger L. (1903). Bolyai János szülőházáról. Mathematikai
és Physikai Lapok 12, 53–56.
[134] Schmidt, F. (1868). Aus dem Leben zweier ungarischer Mathematiker,
Johann und Wolfgang Bolyai von Bolya. Grunerts Archiv der Math. Und Phys.
Greifswald 48, 217–228.
[135] Schmidt, F. (1899). Briefwechsel zwischen Carl Friedrich Gauss
und Wolfgang Bolyai. Leipzig.
[136] Sheehan, J. J. (1994). German History 1770–1866. The Oxford History
of Modern Europe. Clarendon Press, Oxford.
[137] Staar Gy. (1990). A megélt matematika c. kötetben 59–80 old.:
A lámpás ember – Weszely Tibor. Gondolat, Budapest.
[138] Stäckel, P., Engel, F. (1895). Die Theorie der Parallallinien
von Euklid bis auf Gauss. Teubner, Leipzig.
[139] Stäckel P. (1902). Vizsgálatok az absolut geometria köréből Bolyai
János hátrahagyott irataiban. Mathematikai és Természettudományi Értesítő
20, 160–186.
[140] Stäckel P. (1902). Bolyai János észrevételei Lobacsevszkij Miklósnak
a parallelákra vonatkozó vizsgálataira. Matematikai és Természettudományi
Értesítő 20, 40–67.
[141] Stäckel P. és Kürschák J. (1902). Bolyai János észrevételei Lobatschefszkij
Miklósnak a parallelákra vonatkozó vizsgálataira. Matematikai és Természettudományi
Értesítő 20, 41–67.
[142] Stäckel P. (1903). Bolyai János térelmélete. Matematikai és Természettudományi
Értesítő 21, 135–145.
[143] Stäckel, P. (1914). Bolyai Farkas és Bolyai János geometriai vizsgálatai
I–II. Budapest.
[144] Stillwell, J. (1996). Sources of Hyperbolic Geometry. History
of Math. Vol 10, Amer. Math. Soc., London Math. Soc.
[145] Szász P. (1973). Bevezetés a Bolyai–Lobacsevszkij-féle geometriába.
Akadémiai Kiadó, Budapest.[146] Strommer Gy. (1977/1980). A Bolyai geometria
szerkesztéselméletéről. Matematikai Lapok 28, 65–67.
[147] Szabó P. (1903). Az abszolút geometria egyik alaptételéről. Mathematikai
és Physikai Lapok 12, 321–326.
[148] Szász P. (1953). A hiperbolikus trigonometria különböző elemi
előállításai. MTA Mat. Fiz. Tud. Oszt. Közl. 3, 209–225.
[149] Szénássy B. (1960). Bolyai János. A matematika tanítása 7, 34–39.
[150] Szénássy B. (1970). A magyarországi matematika története (A legrégebbi
időktől a 20. század elejéig). Akadémiai Kiadó, Budapest.
[151] Szénássy B. (1975). Bolyai Farkas. Akadémiai Kiadó, Budapest.
[152] Szénássy B. (1978). Kérdések és válaszok. In: Bolyai Jánosra emlékezünk!
TIT Budapesti Szervezete Matematikai Szakosztályának kiadványa, 29–40.
[153] Szénássy B. (1978). Bolyai János. Akadémiai Kiadó, Budapest.
[154] Szénássy B. (1977/1980). Megjegyzések Gauss nemeuklideszi geometriai
eredményeihez. Matematikai Lapok 28, 133–140.
[155] Szénássy B. (1977/1980). Adalékok a két Bolyai fölfedezésének
történetéhez. Matematikai Lapok 29, 71–95.
[156] Szénássy B. (1980/1983). A két Bolyai életútja és a Tentamen tudományos
jelentősége. Matematikai Lapok 31, 3–14.
[157] Szőkefalvi-Nagy, Gy. (1953). Bolyai János szögharmadolása. Matematikai
Lapok 4, 84–86.
[158] Taurinus, F. A. (1826). Geometriae prima elementa. Köln.
[159] Thom, R. (1971). „Modern” Mathematics: An Educational and Philosophic
Error? American Scientist 59, 695–699.
[160] Thurston, W. P. (1982). Three dimensional manifolds, Kleinian
groups and hyperbolic geometry. Bull. (New Series) Amer. Math. Soc. 6,
357–381.
[161] Thurston, W. P. (1997). Three-Dimensional Geometry and Topology,
Vol. I. Princeton University Press, Princeton, N. J.
[162] Toró T. (1973). Nemeuklideszi geometriák a modern fizikában és
a relativisztikus kozmológiában. Korunk Évkönyv, Kolozsvár, 245–256.
[163] Torretti, R. (1996). Relativity and Geometry. Dover, New York.
[164] Tóth Imre (1965). A nemeuklideszi geometria előtörténetéből. Matematikai
Lapok 16, 300–315.
[165] Tóth Imre (2000). Isten és geometria. Osiris, Budapest.
[166] Tymoczko, T. (1998). New Directions in the Philisophy of Mathematics
(revised and expanded paperback edition). Princeton University Press, Princeton
N. J.
[167] Ungar, A. (1997). Thomas Precession: Its Underlying Gyrogroup
Axioms and their use in Hyperbolic Geometry and Relativistic Physics. Foundations
of Physics 27, 881–951.
[168] Ungar, A. (1999). The hyperbolic Pythagorean theorem in the Poincaré
disk model of hyperbolic geometry. The American Mathematical Monthly 106,
759–763.
[169] Varga O. (1953). A Bolyai–Lobacsevszkij-geometria hatása a geometria
fejlődésére. MTA Mat. Fiz. Tud. Oszt. Közl. 3, 151–171.
[170] Vállas A. (1836). Literatúratörténet. Tudománytár, 143–172.
[171] Vekerdi L. (1969). Kalandozás a tudományok történetében. Magvető
Kiadó, Budapest
[172] Vekerdi L. (1981). A Bolyai-kutatás változásai. Természet Világa
112, 56–58.
[173] Vekerdi, L. (2001). A Bolyai-gyűjtemény a Bolyai-kutatásban. Örökségünk,
élő múltunk. Gyűjtemények a Magyar Tudományos Akadémia Könyvtárában. MTA
Könyvtára, Budapest, 85–114.
[174] Weszely Tibor (1974). Bolyai Farkas, a matematikus. Tudományos
Könyvkiadó, Bukarest.
[175] Weszely Tibor (1981). Bolyai János matematikai munkássága. Kritérion,
Bukarest.
[176] Weszely Tibor (1980/1983). Bolyai János kéziratban hátrahagyott
matematikai munkáiról. Matematikai Lapok 31, 29–37.
[177] Weszely T. (1985). Bolyai János emlékezete. In: Bolyai Jánosra
emlékezünk! TIT Budapesti Szervezete Matematikai Szakosztályának kiadványa.
 Lobacsevszkij
közleményeit a szakmai és a nem szakmai közvélemény egyaránt érdektelenséggel
fogadta. Bolyainál nem ez volt a helyzet, ő még letaglózást is kapott hozzá,
Gausstól. Ám másoknak azért lehetett pozitív véleménye Bolyai művéről.
Talán a leghivatottabb testület, a Magyar Tudós Társaság Mathematikai Osztálya
kifejezte valamiképpen elismerését? Vállas Antal akadémikus 1836-ban összefoglaló
cikket írt a hazai matematika addigi eredményeiről. Hosszasan panaszkodik,
hogy nehéz sorsunk volt; tatár, török stb., ezért nem tudtunk eléggé fejlődni.
Bolyaival kapcsolatban idézi a Tentamen, Az arithmetica eleje és Az arithmeticának,
geometriának és physikának eleje című műveket. A szövegben csak annyit
ír, hogy „Bolyai különcségével tűnik ki”. A művek felsorolásából látjuk,
hogy Farkasról, nem pedig Jánosról van szó. Ámde a Tentamen címében benne
van, hogy „Cum Appendice Triplici”, tehát valamiképpen mégis szerepel János
műve is a felsorolásban? Sajnos, ez sem áll. Az említett három függelék
a második kötethez tartozik, vagyis a teljes könyv végén van. A Tentamenhez
készített magyar nyelvű prospektus tájékoztatta a vásárlókat arról, hogy
a jelzett három függelék hol található. E szerint Bolyai János művét Vállas
Antal összefoglaló cikke nem említi, az irodalomjegyzékben sem szerepel.
Azt, hogy az összefoglaló cikk szerzője nem értette meg Bolyai János alkotásának
lényegét és jelentőségét, még el lehet fogadni. Azt azonban már nem, hogy
említést sem tesz róla. Pedig Bolyai Farkas a Tentament 1832-ben megküldte
a Magyar Tudós Társaságnak, és az ott porosodott a könyvtár polcain.
Lobacsevszkij
közleményeit a szakmai és a nem szakmai közvélemény egyaránt érdektelenséggel
fogadta. Bolyainál nem ez volt a helyzet, ő még letaglózást is kapott hozzá,
Gausstól. Ám másoknak azért lehetett pozitív véleménye Bolyai művéről.
Talán a leghivatottabb testület, a Magyar Tudós Társaság Mathematikai Osztálya
kifejezte valamiképpen elismerését? Vállas Antal akadémikus 1836-ban összefoglaló
cikket írt a hazai matematika addigi eredményeiről. Hosszasan panaszkodik,
hogy nehéz sorsunk volt; tatár, török stb., ezért nem tudtunk eléggé fejlődni.
Bolyaival kapcsolatban idézi a Tentamen, Az arithmetica eleje és Az arithmeticának,
geometriának és physikának eleje című műveket. A szövegben csak annyit
ír, hogy „Bolyai különcségével tűnik ki”. A művek felsorolásából látjuk,
hogy Farkasról, nem pedig Jánosról van szó. Ámde a Tentamen címében benne
van, hogy „Cum Appendice Triplici”, tehát valamiképpen mégis szerepel János
műve is a felsorolásban? Sajnos, ez sem áll. Az említett három függelék
a második kötethez tartozik, vagyis a teljes könyv végén van. A Tentamenhez
készített magyar nyelvű prospektus tájékoztatta a vásárlókat arról, hogy
a jelzett három függelék hol található. E szerint Bolyai János művét Vállas
Antal összefoglaló cikke nem említi, az irodalomjegyzékben sem szerepel.
Azt, hogy az összefoglaló cikk szerzője nem értette meg Bolyai János alkotásának
lényegét és jelentőségét, még el lehet fogadni. Azt azonban már nem, hogy
említést sem tesz róla. Pedig Bolyai Farkas a Tentament 1832-ben megküldte
a Magyar Tudós Társaságnak, és az ott porosodott a könyvtár polcain.




