A bolygók mozgását sokáig a pontosság, az égi harmónia megtestesítőjének tartották. Az utóbbi években azonban kiderült, hogy a Naprendszer dinamikája számos vonásában kaotikus. Kaotikus viselkedéssel a nemrégiben felfedezett exobolygórendszerekben is találkozhatunk. A bolygórendszerek kaotikus dinamikai jelenségeinek vizsgálata mára az égi mechanika egyik fő kutatási területévé vált. Az ezen a téren elért fontosabb eredményeket mutatja be ez a cikk.
 
 

A bolygók mozgása a Naprendszerben

A naprendszerbeli kaotikus jelenségek kutatása mintegy két évtizede kezdődött. Ekkorra érték el a számítógépek azt a teljesítőképességet, amely már lehetővé tette a szükséges hosszú időtartamú numerikus integrálások elvégzését, illetve ekkorra születtek meg az első káoszdetektálási módszerek. Azt, hogy a Naprendszerben kaotikus viselkedés lehetséges, már korábban sejtették. H. Poincaré már a XIX. század végén felfedezte, hogy a háromtest-probléma bizonyos megoldásai igen „vadul” viselkednek. A XX. század közepén A. N. Kolmogorov, V. I. Arnold és J. Moser munkássága nyomán kifejlődött KAM-elmélet rávilágított arra, hogy a legalább két szabadsági fokú, nemlineáris rendszerekben a reguláris mozgások mellett kaotikus mozgások is lehetségesek. A kaotikus viselkedés kialakulása szempontjából kitüntetett szerepük van a rezonanciáknak. Ezeknek, miként egy ingának, lehetnek stabil és instabil egyensúlyi pontjai. (Ha egy inga nyugalomban van, függőlegesen lóg, stabil egyensúlyi helyzetet vesz fel. Ha az ingát lengetve a kitérés amplitúdóját 180°-ra növeljük, az inga függőlegesen álló, de instabil egyensúlyi helyzetbe kerül, ahonnan a legkisebb zavaró hatás kitéríti.) A mozgás különösen érzékeny a kezdőfeltételekre az instabil egyensúlyi pontok közelében; perturbált, zavart rendszerekben ezeken a helyeken a mozgás kaotikus. A Naprendszerben számos rezonancia található, ezek közelében, a KAM-elmélet értelmében, kaotikus viselkedést vártak. Ennek kimutatása azonban nem könnyű, így a KAM-elmélet megszületése után még jó néhány évnek el kellett telnie, míg a feltételek megértek a naprendszerbeli kaotikus jelenségek vizsgálatára.

A bolygók mozgását a Nap körül első közelítésben a jól ismert Kepler-törvények írják le. A bolygómozgások Kepler-modellje a bolygórendszert tökéletesen stabilnak mutatja: a bolygók változatlan ellipszispályákon keringenek a Nap körül, a rendszer úgy működik, mint egy nagy óramű.

Ez a modell azonban csak akkor lenne érvényes, ha minden egyes bolygóra egyedül a Nap gravitációs vonzása hatna. A valóságban, a Newton-féle általános tömegvonzási törvénynek megfelelően, gravitációs kölcsönhatás a bolygók között is fellép. Ennek hatására pályájuk megváltozik, mozgásuk bonyolult, nehezen kiszámítható lesz. A bolygópályákat jellemző pályaelemek változásainak, perturbációinak meghatározására különféle perturbációszámítási módszereket alkalmaznak. A bolygópályák fő változásait a Laplace–Lagrange-elmélet írja le. Ez a bolygórendszer viselkedését véges számú periodikus mozgás szuperpozíciójaként előálló, feltételesen periodikus (másképp kváziperiodikus) megoldással közelíti. (Nem biztos, hogy a különféle frekvenciájú periodikus mozgások összetevéséből eredő mozgás periodikus lesz; ennek az a feltétele, hogy a frekvenciák aránya racionális legyen, a periodikusság tehát feltételhez kötött.) Az egyes periódusokhoz tartozó frekvenciák a Naprendszer fundamentális vagy szekuláris sajátfrekvenciái. Ezek értéke igen kicsi, így a szekuláris periódusok igen hosszúak, ténylegesen 45 000 év és 2 millió év közé esnek. A bolygók kölcsönös perturbációinak hatására a bolygók pályaellipszisei, illetve pályasíkjai ekkora periódusidőkkel lassan körbefordulnak (a pályaellipszisek a pálya menti keringéssel megegyező, a pályasíkok azzal ellentétes irányban), miközben a pályák hajlásszögei és excentricitásai kváziperiodikus ingadozásokat végeznek. A Laplace–Lagrange-elméletben szereplő konstansokat (amplitúdók, frekvenciák, fázisok) a megfigyelési adatok pontosabbá válásával és az elmélet többszöri továbbfejlesztésével az idők folyamán sokszor újraszámították. Az elméletnek egyrészt fontos alkalmazásai vannak, többek között a Föld hosszú távú pályaelem-változásaitól függő jelenségek, például az éghajlati változások kutatásában, másfelől az elméletnek máig akadnak lezáratlan problémái, így a szekuláris sajátfrekvenciák pontos meghatározása ma is aktuális kérdés.

A Laplace–Lagrange-elmélet is stabilnak írja le a bolygórendszert, kérdés azonban, hogy ez a feltételesen periodikus közelítés milyen pontosan felel meg a valóságnak. Ennek eldöntéséhez ki kellene számítani az összes többi perturbációt, ez azonban analitikus módszerekkel nem lehetséges. Mivel a bolygók mozgását meghatározó mozgásegyenletek analitikusan nem integrálhatók (azt, hogy a „legegyszerűbb eset” – a háromtest-probléma – nem integrálható, Poincaré bizonyította be), analitikus megoldást végtelen sorok formájában próbáltak levezetni. E sorokról azonban bebizonyosodott, hogy nem mindig konvergensek, így ezekkel a bolygórendszer mozgását nem lehet tetszőlegesen hosszú időre megadni. A problémát az úgynevezett kis nevezők okozzák. A sorfejtések együtthatóiban a mozgást jellemző frekvenciák lineáris kombinációi lépnek fel, és rezonanciák közelében, ahol a frekvenciák aránya racionális, e kifejezések tetszőlegesen kicsik lehetnek. A rezonanciák közelében a kis nevezők a perturbációs sorokat divergenssé teszik. Fizikai szempontból a divergencia oka az, mint arra a KAM-elmélet rámutatott, hogy perturbált rendszerek rezonanciái közelében a fázistér szerkezete igen bonyolult, a mozgás kaotikus, és ezt konvergens sorokkal nem lehet megadni. A bolygók perturbált mozgására levezetett sorfejtések tehát szigorú matematikai szempontból nem jók, ám a gyakorlatban mégis használják ezeket. A tapasztalat ugyanis az, hogy ezen sorfejtések első tagjainak (esetenként néhány száz tagnak) a segítségével a bolygók mozgása jól közelíthető a gyakorlati alkalmazások céljaira egy nem túl hosszú, néhány évtizedes időintervallumban. Ennek hossza azonban előre nem ismeretes, így ebből a közelítő megoldásból a bolygók mozgására nézve hosszabb időre következtetéseket nem lehet levonni.

Mivel a bolygórendszer viselkedését hosszú távra analitikus módszerekkel nem sikerült meghatározni, amint erre lehetőség nyílt, a mozgásegyenletek numerikus integrálásához folyamodtak. Az első ilyen, hosszú időtartamra kiterjedő számítást a külső nagybolygókra végezték, elsősorban a Plútó mozgásának meghatározására. A Plútó ugyanis mind méretét, mind pályáját tekintve „kilóg” a külső nagybolygók sorából. Tömege igen kicsi, pályája erősen elnyúlt, nagy pályahajlású ellipszis, melynek napközelpontja (az ekliptika síkjára vetítve) a Neptunusz pályáján belülre esik. (Ma már tudjuk, hogy a Plútó tulajdonképpen a Neptunuszon túli népes kisbolygóövezet, az Edgeworth–Kuiper-öv elsőként felfedezett, legnagyobb tagja.) 1972-ben J. Cohen és munkatársai 1 millió évre integrálták a Jupiter, a Szaturnusz, az Uránusz, a Neptunusz és a Plútó mozgásegyenleteit. Az 1980-as évek közepén a külső bolygórendszer vizsgálatára a Massachusettsi Műszaki Egyetemen külön paralel számítógépet építettek, ez volt a Digital Orrery. Ezzel 1986-ban J. H. Applegate és munkatársai 210 millió évre, majd 1988-ban G. J. Süssman és J. Wisdom 875 millió évre integrálták a külső bolygók mozgásegyenleteit. Ez a számítás mutatta ki először, hogy a Plútó mozgása kaotikus, Ljapunov-ideje 20 millió év (lásd később).

A teljes bolygórendszer mozgásegyenleteinek hosszú időtartamra történő numerikus integrálása igen nehéz feladat. Egy rendszer integrálásakor mindig a legrövidebb keringési periódushoz kell igazítani a lépésközt. A külső nagybolygók esetében a lépésköz 40 napnak választható. A belső nagybolygókat is figyelembe véve a Merkúr jelenléte miatt 0,5 napos lépésköz szükséges. A kis lépésköz miatt nő az integrációs lépések száma, ami a lépésenkénti hiba összegződésével csökkenti a számítások pontosságát.

A teljes bolygórendszer mozgásegyenleteinek hosszú idejű numerikus integrálásával kapcsolatos nehézségeket J. Laskar (1989, 1996) oly módon hidalta át, hogy nem az eredeti mozgásegyenleteket, hanem azoknak a rövid periódusú változásokra nézve kiátlagolt közelítését vizsgálta. Az átlagolt rendszer egyenleteit számítógép segítségével igen nagy pontossággal vezette le (a bolygók tömegére nézve a másodrendű, az excentricitásokra és pályahajlásokra nézve az ötödrendű tagokat is figyelembe vette), így az egyenletek valamivel több mint 150 000 tagot tartalmaztak. Mivel azonban ezek a tagok már csak a szekuláris sajátfrekvenciáktól függnek, a hosszú periódusidők miatt ennek az úgynevezett szekuláris rendszernek a numerikus integrálása 500 éves lépésközzel lehetséges. A több száz millió évre kiterjedő integrálásnál így a lépések száma jelentősen csökkenthető. (Az egyenletek jobb oldalán szereplő nagyszámú tag nem okoz különösebb problémát az egyenletek szimmetrikus alakja miatt.) Laskar a szekuláris rendszert 200 millió évre numerikusan integrálta, és azt az eredményt kapta, hogy nemcsak a Plútó, hanem a belső bolygók mozgása is kaotikus; a Merkúr, a Vénusz, a Föld és a Mars esetében a Ljapunov-idő mindössze 5 millió év! Ugyanakkor a külső nagybolygók, a Jupiter, a Szaturnusz, az Uránusz és a Neptunusz mozgása reguláris.

Egy pálya kaotikussága számszerűleg a Ljapunov-exponensekkel jellemezhető. Ezek azt a tapasztalatot fejezik ki egzakt formában, hogy a fázistér reguláris tartományaiban a közeli kezdőpontokból kiinduló trajektóriák lineárisan távolodnak egymástól, míg a kaotikus tartományokban a trajektóriák eltérése exponenciálisan nő. Egy n szabadsági fokú rendszerben egy trajektóriának n számú Ljapunov-exponense van. Egy pálya akkor kaotikus, ha van legalább egy pozitív Ljapunov-exponense. A pályák jellegének vizsgálatakor általában elég a legnagyobb Ljapunov-exponenst kiszámítani, amit l-val szokás jelölni, hiszen ha l pozitív, a pálya kaotikus, ha negatív, a pálya reguláris. A l reciproka a Ljapunov-idő, ezt T_L-lel jelölve T_L=1/l. Két pálya eltérése a fázistérben közelítőleg (elegendően nagy t-re) a

d=d₀e^t/TL

összefüggéssel adható meg, ahol d₀ a két pálya közti kis eltérés a kezdőpillanatban, d pedig az eltérés t idő múlva (e=2,718… a természetes logaritmus alapszáma). T_L idő alatt a kezdeti eltérés e-szeresére nő. Minél kisebb T_L, a közeli fázispontokból induló trajektóriák annál gyorsabban távolodnak egymástól.

Mit jelent az, hogy a belső bolygók és a Plútó mozgása kaotikus? Azt, hogy mozgásuk igen érzékenyen függ a kezdőfeltételektől. Ha jelenlegi helyzetük kissé más lenne, mozgásuk tökéletesen másként alakulna. Ha például a Föld helyzete a jelenlegitől igen kicsivel, például 15 méterrel különbözne, vagy másként fogalmazva, ha ekkora a hiba a Föld kezdőpozíciójában, akkor (mivel T_L=5 millió év) az exponenciális növekedés miatt a hiba kb. 150 m-re nő 10 millió év alatt, de 150 millió km lesz 100 millió év múlva! (Ez kb. akkora, mint a Nap–Föld távolság.) Így elfogadható pontosságú előrejelzéseket csak mintegy 10 millió éves időtartamra lehet készíteni, lehetetlen azonban a belső bolygók és a Plútó pálya menti helyzetét 100 millió évre előre pontosan kiszámítani!

A kaotikus viselkedést a belső bolygók esetében a szekuláris sajátfrekvenciák közti szekuláris rezonanciák okozzák. Szekuláris rezonanciáról beszélünk, ha a sajátfrekvenciák valamilyen lineáris kombinációja közelítőleg nulla. A szekuláris rezonancia legegyszerűbb esete, ha két égitest pályaellipszise vagy pályasíkja közelítőleg azonos szögsebességgel forog. A belső bolygók kaotikus viselkedéséért a

2g₄–2g₃–s₄+s₃ť0,         g₁–g₅–s₁+s₂ť0

szekuláris rezonanciák a felelősek, ahol g_l, g₃, g₄, g₅ közelítőleg a Merkúr, a Föld, a Mars és a Jupiter perihélium-mozgásának frekvenciái, s_l, s₂, s₃, s₄ közelítőleg a Merkúr, a Vénusz, a Föld és a Mars pályasíkjának precessziós frekvenciái. Kimutatható, hogy az ezekhez a rezonanciákhoz tartozó szögváltozók (olyan forgásszög jellegű változók, melyek frekvenciái 2g₄–2g₃–s₄+s₃, illetve g₁–g₅–s_l+s₂) időbeli viselkedése a szekuláris sajátfrekvenciák változásai következtében libráció és cirkuláció között váltakozik, ami tipikus jelenség kaotikus viselkedés esetén. (Ismét az ingahasonlattal élve: libráció az inga lengő mozgása; cirkuláció esetén az inga körbeforog. Perturbált rendszerekben a káosz egyik megnyilvánulása lehet, hogy bizonyos mennyiségek viselkedése rendszertelenül váltakozik libráció és cirkuláció között.) E váltakozás következtében a pályák térbeli orientációját megadó szögek egy idő után tökéletesen határozatlanná válnak, a pálya menti helyzetet ezért nem lehet előre jelezni. Másfelől e rezonanciák jelenléte gátolja meg, hogy a pályaelemek változásaira kapott idősorokra feltételesen periodikus megoldást illeszthessünk; azok kaotikus jellegűek. Megjegyezzük, hogy a Plútó esetében is több rezonancia jelenléte okozza mozgásának a kezdőfeltételekre való nagyfokú érzékenységét.

Jóllehet a külső óriásbolygók mozgása több száz millió évre reguláris, viselkedésük feltételesen periodikus megoldással közelíthető, azonban ezek is közel vannak olyan középmozgás-rezonanciákhoz, melyekben mozgásuk kaotikus lenne (a középmozgás az átlagos pálya menti szögsebesség). A Jupiter és Neptunusz közötti tartományt kettes és hármas középmozgás-rezonanciák hálózzák be sűrűn. Ezek a rezonanciák a bolygók környezetét kaotikussá teszik.
 

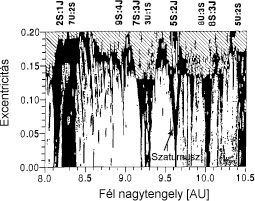
1. ábra. A Szaturnusz környezetének rezonáns szerkezete (Michtchenko és társai, 2001)

Példaként az 1. ábrán a Szaturnusz környezetét mutatjuk be Michtchenko és társai (2001) vizsgálatai alapján. A vízszintes, illetve függőleges tengelyen a Szaturnusz-pálya jelenlegi fél nagytengelye, illetve excentricitása körül adtunk meg egy-egy tartományt. A Szaturnusz jelenlegi pályaadatainak megfelelő pontot az ábrán nyíl jelzi. Az ábra minden pontjának egy kezdeti fél nagytengely- és egy excentricitásérték feleltethető meg. Egy ilyen kezdőponthoz a Szaturnusz többi pályaelemét változatlanul hozzávéve numerikusan integrálhatók az így definiált fiktív Szaturnusz mozgásegyenletei a Jupiter, az Uránusz és Neptunusz perturbáló hatásának figyelembevételével. Az integrálást elegendően hosszú időre (az adott esetben 1,5ˇ10⁶ évre) elvégezve káoszdetektálási módszerekkel meghatározható, hogy a fiktív Szaturnusz mozgása milyen mértékben kaotikus. Az integrálást más kezdőpontokra megismételve az ábra minden pontjához hozzá lehet rendelni az azon pontból induló fiktív Szaturnusz-pálya kaotikusságának mértékét. Az egyszerű ábrázolás kedvéért a kaotikusság jellemzésére szürke színskálát alkalmaztunk: az ábrán a világosabb árnyalatok kevésbé, a sötétebbek erősebben kaotikus pályákat jelentenek. A sötét kaotikus sávok középmozgás-rezonanciáknak felelnek meg. Az ábra felső részén van feltüntetve, hogy mely rezonanciákról van szó (a J, S, U, N betűk az egyes bolygókra vonatkoznak, a 2S:1J kifejezés pl. a Szaturnusz és a Jupiter középmozgása közötti 2:1 arányú rezonanciát jelenti). A világos tartományokban a mozgás reguláris. Látható, hogy a valódi Szaturnusz az egyik reguláris tartományban helyezkedik el, azonban igen közel van a Szaturnusz és a Jupiter közötti 5:2 arányú rezonanciához. Ha a Szaturnusz pályájának fél nagytengelye 0,03 AU-val (csillagászati egységgel) nagyobb lenne, a Szaturnusz az 5:2 arányú rezonanciában foglalna helyet, és mozgása kaotikus lenne. Az 5:2 rezonanciába eső kezdőpontokkal végzett, hosszú időtartamra kiterjedő numerikus integrálás azt mutatja, hogy a pályák kaotikusak, ám több száz millió évig stabilak maradhatnak. (Ez az úgynevezett stabil káosz egy esete, amikor a pályaelemek változásának jellege kaotikus, ám a változások mértéke szűk korlátok közé esik. Így bár a mozgást pontosan nem lehet előre jelezni, a pályák bizonyos tartományon belül maradva megőrzik stabilitásukat.) Ha azonban excentricitásuk 0,15 fölé nő, a rendszer néhány millió év alatt instabillá válik a bolygók közt bekövetkező szoros megközelítések vagy ütközések következtében. Az ábrán a satírozás ilyen instabil tartományokat jelöl.

Hasonló kép vázolható a többi óriásbolygóról is. A Jupiter is igen közel esik a Szaturnusszal való 5:2-es rezonanciához. Az Uránusz egy olyan tartományban foglal helyet, melyet egyik oldalról a Jupiterrel való 7:1-es és a Neptunusszal való 2:1-es rezonancia, másik oldalról a Szaturnusszal való 3:1-es rezonancia határol. A Neptunusz az Uránusszal való 2:1-es rezonanciához van közel. Ezekben a rezonanciákban a bolygók mozgása kaotikus lenne, ám több száz millió évig excentricitásuk kicsi maradna, és így képesek lennének elkerülni az egymással való ütközéseket.

A külső Naprendszer tehát nagymértékben rezonáns szerkezetű. A külső Naprendszer kialakulásának utolsó fázisában a bolygók kisebb-nagyobb vándorutat tettek meg, míg jelenlegi pályájukat elfoglalták, és ennek során időszakosan rezonanciába kerülhettek egymással. Jelenleg kutatások tárgya, hogy a rezonanciák hogyan befolyásolták a külső nagybolygók pályáinak dinamikai fejlődését, vagy az időszakos rezonanciák milyen hatással voltak egyéb naprendszerbeli objektumokra, például a kisbolygókra.

A bolygók és holdak tengelyforgása

A Naprendszerben elsőként megfigyelt kaotikus jelenség a Szaturnusz egyik holdjának, a Hyperionnak a kaotikus rotációja volt, melyet a Voyager–1 űrszonda mérései alapján fedeztek fel 1981-ben. Amikor a Hyperion fénygörbéjét megvizsgálták, kiderült, hogy arra semmiféle periodikus vagy kváziperiodikus görbét nem lehet illeszteni, a fénygörbe kaotikusan változik (Wisdom és társai, 1984, Klavetter, 1989). A Hyperion kisméretű, szabálytalan alakú hold (alakját háromtengelyű ellipszoiddal közelítve a tengelyek mérete 185´140´113 km). A bolygók holdjainak tengelyforgását a dagálysúrlódás szinkronizálja; ez a folyamat a Hyperiont kivéve már valamennyi holdnál lezajlott. Szabálytalan alakú holdaknál a keringés-rotáció rezonanciát a fázistérben (a helyzetet és mozgásállapotot jellemző változók terében) kiterjedt kaotikus zóna veszi körül. A holdaknak a szinkronizáció előtt ezen kellett áthaladniuk. A Hyperion jelenleg is ebben a kaotikus zónában tartózkodik. Forgástengelyének iránya és szögsebessége rendszertelenül változik; rövid időre, a hold néhány keringésére sem lehet előre jelezni (a Hyperion keringési ideje 21 nap).

A Hyperion esete nyomán megújult az érdeklődés a bolygók tengelyforgásának problémája iránt is. J. Laskar és munkatársai (1993) azt vizsgálták, hogyan változik a Föld forgástengelyének iránya a Nap és a Hold forgatónyomatékának, valamint a planetáris perturbációknak a hatására. A Föld forgástengelye a Nap és a Hold együttes hatására egyrészt precessziós mozgást végez az ekliptika pólusa körül, kb. 50”/év precessziós szögsebességgel, másfelől a forgástengelynek az ekliptikával bezárt szöge is módosul annak következtében, hogy a bolygók perturbálják a Föld pályáját, az ekliptikát. Ezt a változást az ekliptika és az egyenlítő közti dőlésszög alakulásával szokás kifejezni. A dőlésszög változása igen nagy jelentőségű a hosszú távú éghajlati hatások szempontjából. Laskar és munkatársai a kezdőfeltételek sokasága mellett 18 millió évre numerikusan integrálták a forgástengely precessziós mozgását és az ekliptika dőlésszögének változását meghatározó precessziós mozgásegyenleteket. Az ekliptika kezdeti dőlésszögét 0–125° között – 0,1°-os lépésközzel változtatva – minden kezdőértékhez meghatározták a precessziós paraméterek fejlődését. Kiderült, hogy ha a kezdeti dőlésszög 60–90° közé esne, mind a dőlésszögben, mind a forgástengely precessziós szögsebességében nagy amplitúdójú kaotikus változások lépnének fel. Mivel az ekliptika jelenlegi dőlésszöge 23,3°, ez kívül esik a kaotikus tartományon. A számítások szerint a dőlésszög 23,3°-os kezdőértéke esetén a dőlésszögben ą18 millió év alatt ą1,3°-os változások lehetségesek. Ezeknek a látszólag kis ingadozásoknak számottevő hatása lehet az éghajlat változására. Kiszámítható, hogy a dőlésszög 1,3°-os változása mintegy 20%-kal módosíthatja a nyári szoláris besugárzás mértékét 65°-os északi földrajzi szélességen. Ez azért figyelemre méltó, mert a jégkorszakok Milankovic-elmélete szerint a magas földrajzi szélességeken bekövetkező nyári hőmennyiség-módosulásnak döntő szerepe van az éghajlat hosszú távú változásaiban.

A precessziós egyenletek numerikus integrálásával folytatott vizsgálatok rávilágítottak a Holdnak a földi életfeltételek biztosításában játszott meghatározó szerepére is. A Föld forgástengelyének precessziós frekvenciáját a Nap és a Hold forgatónyomatékának együttes hatása határozza meg. Ha a Hold nem létezne, a precessziós frekvencia a harmadára csökkenne. Ez az érték közel esik az ekliptika planetáris perturbációinak szekuláris frekvenciáihoz. A forgástengely precessziós frekvenciája több planetáris szekuláris frekvenciával is rezonanciába kerülhetne, és ez az ekliptika dőlésszögének nagymértékű kaotikus ingadozására vezetne a kezdeti dőlésszög széles, 0–85° közti tartományában. A változások mértéke, a jelenlegi 23,3° dőlésszög esetén, egymillió év alatt tíz foknál is nagyobb lehetne (2. ábra). Ennek beláthatatlan következményei lennének a földi éghajlat alakulására. A Hold szerepe tehát az, hogy stabilizálja a Föld forgástengelyének precessziós frekvenciáját a jelenlegi értéknél, és távol tartsa az ekliptika planetáris szekuláris frekvenciáitól, elkerülvén így a dőlésszög kaotikus ingadozására vezető rezonanciákat.
 

2. ábra. Az ekliptika dőlésszögének változása, ha a Hold hatása egy pillanattól kezdve (az ábrán ez a 0 időpont) megszűnne (Laskar és társai, 1993)

A precessziós egyenletek hosszú időtartamú numerikus integrálását a többi bolygóra is elvégezték. E vizsgálatok arra a meglepő eredményre vezettek, hogy a Mars egyenlítőjének és pályasíkjának dőlésszöge jelenleg kaotikusan változik, a változások mértéke néhány millió év alatt 30-40° is lehet. Mind a Merkúr, mind a Vénusz tengelyforgása jelentős kaotikus fejlődésen mehetett át, míg jelenlegi állapotuk kialakult. A Vénusz tengelyforgása abból a szempontból különleges, hogy a többi bolygótól eltérően a Vénusz a pálya menti keringéssel ellenkező irányban, „visszafelé” forog. Ezért sokan azt gondolják, hogy a Vénusz „fejjel lefelé” született. Azonban lehetséges, hogy forgástengelyét a kaotikus fejlődés vitte pályasíkjának közelébe, ahonnan azután disszipatív erők hatására került a jelenlegi állapotba (ez utóbbi hatások vizsgálata már kivezet a KAM-elmélet köréből). A vizsgálatok szerint a külső nagybolygók tengelyforgása alapvetően stabil. Ennek oka, hogy a precessziós frekvenciák és a pályasíkok planetáris perturbációinak szekuláris frekvenciái jól elkülönülnek, közöttük rezonanciák nem lehetségesek.

(Az írás második részét következő számunkban közöljük.)